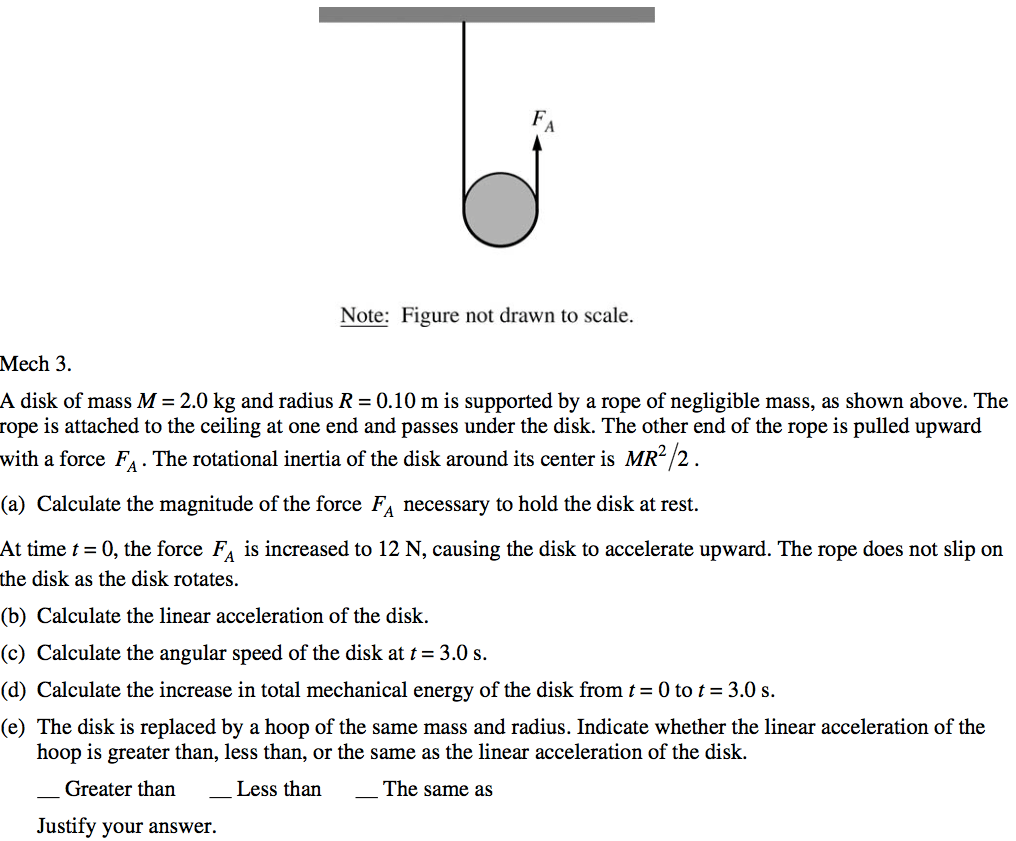
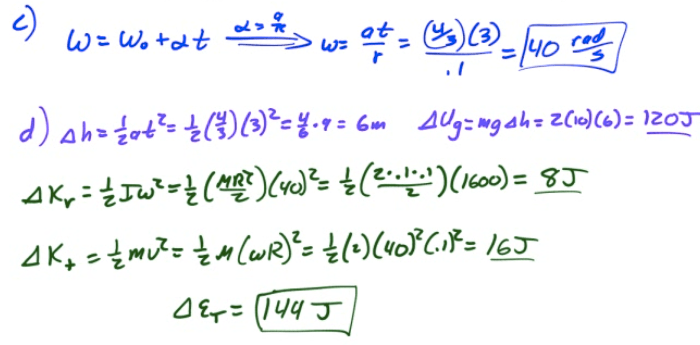Conservational of Energy
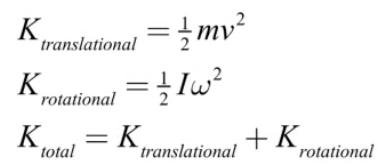
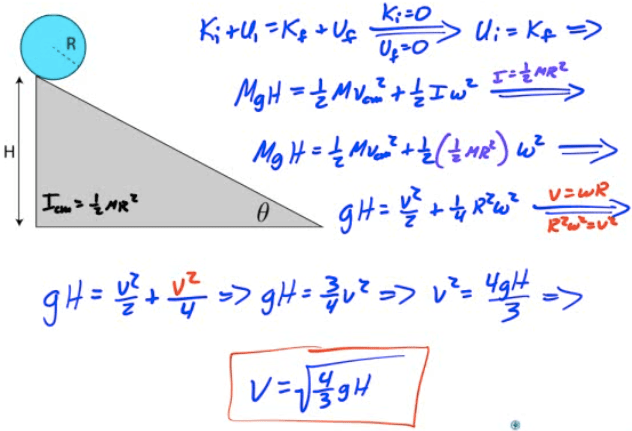
Example 1: Disc Rolling Down an Incline
Find the speed of a disc of radius R which starts at rest and rolls down an incline of height H
Rotational Dynamics
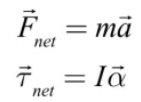
Example 2: Strings with Massive Pulleys
Two blocks are connected by a light string over a pulley of mass mp</sub and radius R.
Find the acceleration of mass m2</sub if m1</sub stis on a frictionless surface
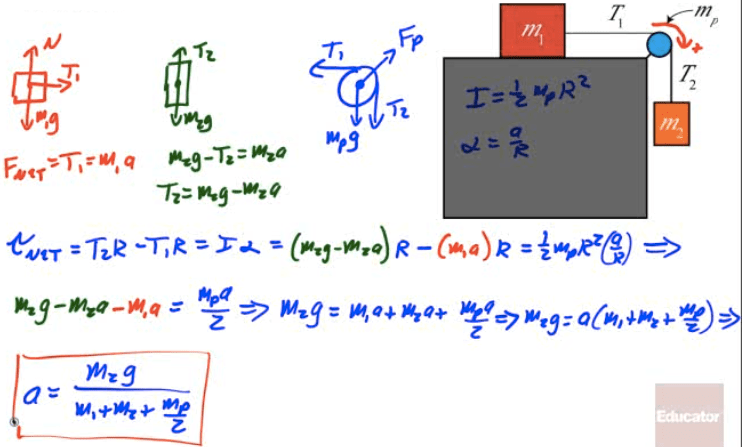
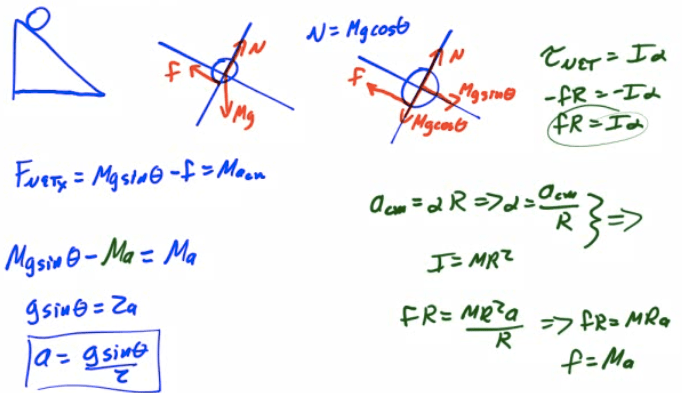
Example 3: Rolling Without Slipping
A disc of radius R rolls down an incline of angle θ without slipping.
Find the force of friction on the disc
Example 4: Rolling with Slipping
A bowling ball of mass M and radius R skids horizontally down the alley with an initial velocity of v0. Find the distance the ball skids before rilling given a coefficient of kenetic friction μk


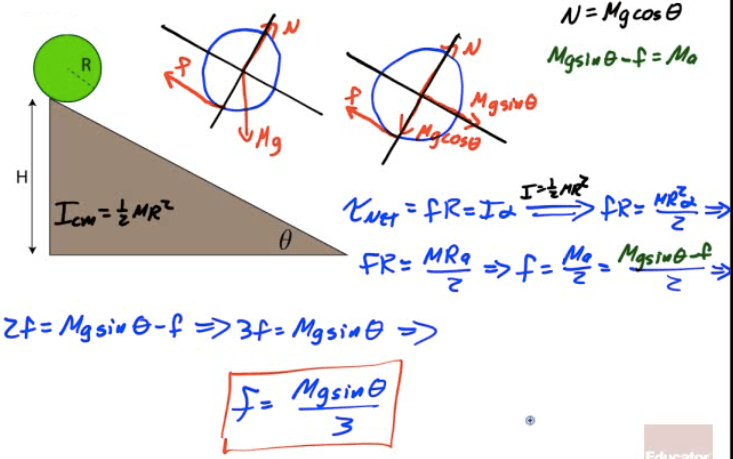
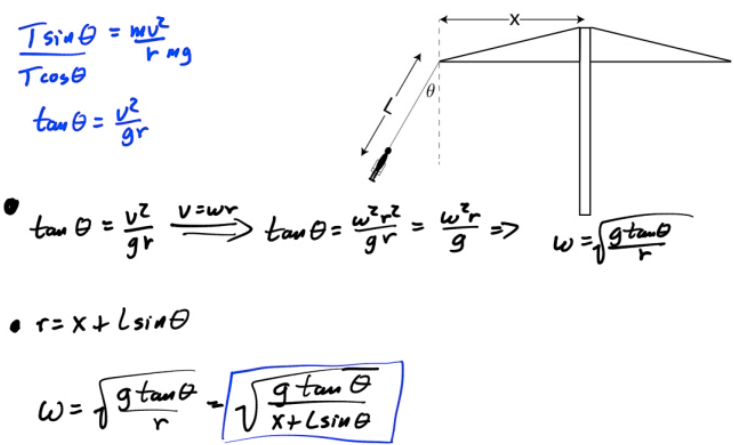
Example 5: Amusement Park Swing
An amusement park ride of radius x allows children to sit in a spinning swing held by a cable of length L.
At maximum angular speed, the cable makes an angle of θ with the vertical as shown in the diagram below
Determine the maximum angular speed of the rider in terms of g, θ, x and L.
2002 Free Response Question 2
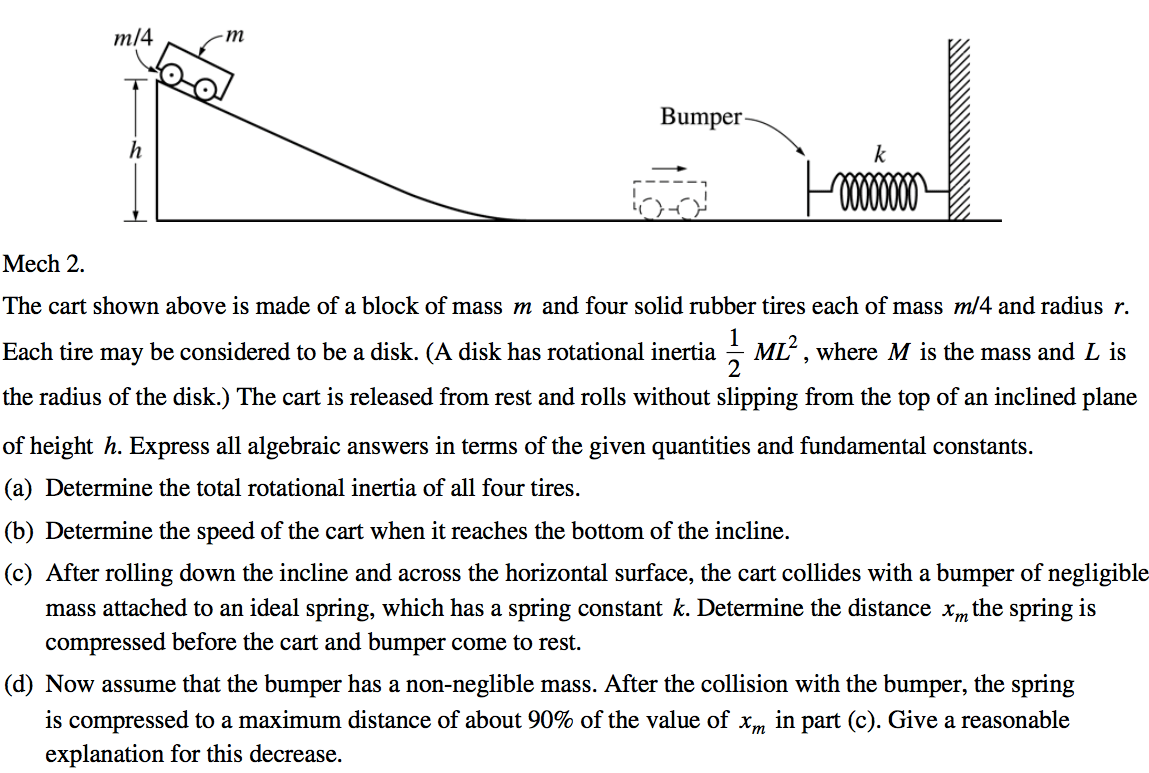

2006 Free Response Question 3

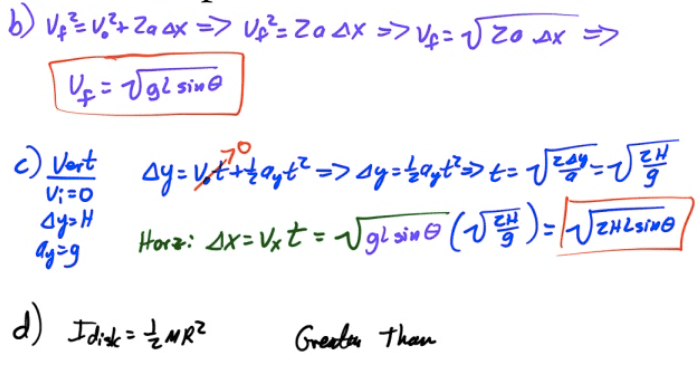
2010 Free Response Question 2
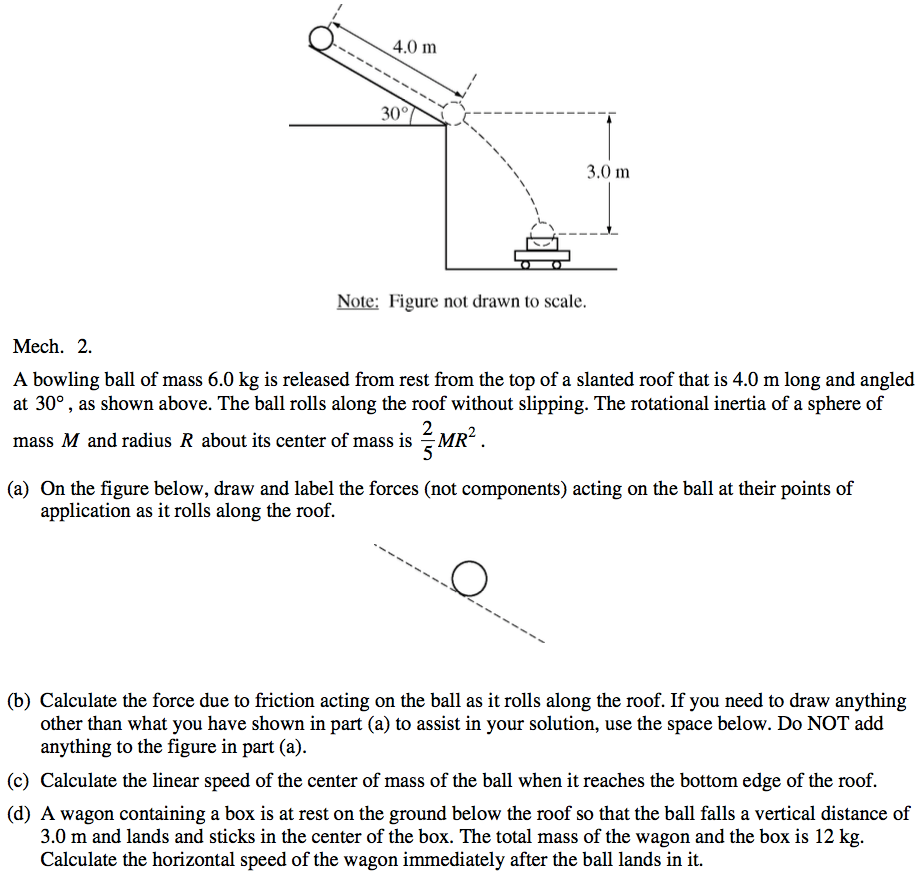
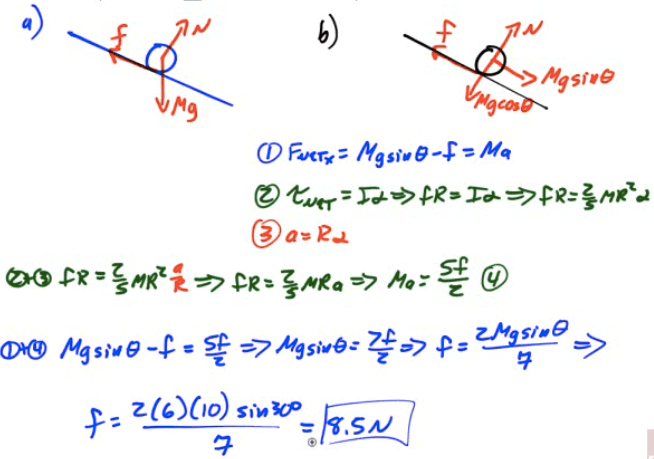

2013 Free Response Question 3